人手不足でお悩みの方は
\ こちらの記事がおすすめ! /
RSA暗号とは?

RSA暗号とは、現在のインターネットの基礎となっている素因数分解を利用した暗号アルゴリズムです。
暗号アルゴリズムでは、桁数の大きな素数を掛け合わせた数字の素因数分解が難しい仕組みを応用しています。
また、RSAは下記の発明者の頭文字を取って名付けられました。
- Ronald Rivest(ロナルド・リベスト)
- Adi Shamir(アディ・シャミア)
- Leonard Adleman(レオナルド・エーデルマン)
暗号アルゴリズムの例として、「6,887」という数字を素因数分解する場合、3もしくは7で割っていくことが一般的です。
4桁の数字でも、「97」「71」の素因数にたどり着くことは困難なため、数百桁の素因数分解を求められるRSA暗号は、パソコンを利用しても非常に困難です。
たしかにパソコンであれば、膨大な時間をかければ素因数分解を計算して解読できてしまいます。
しかし解読できる頃には、情報の価値がなくなっている理由から、暗号として機能するわけです。
公開鍵暗号方式のアルゴリズムの1つ
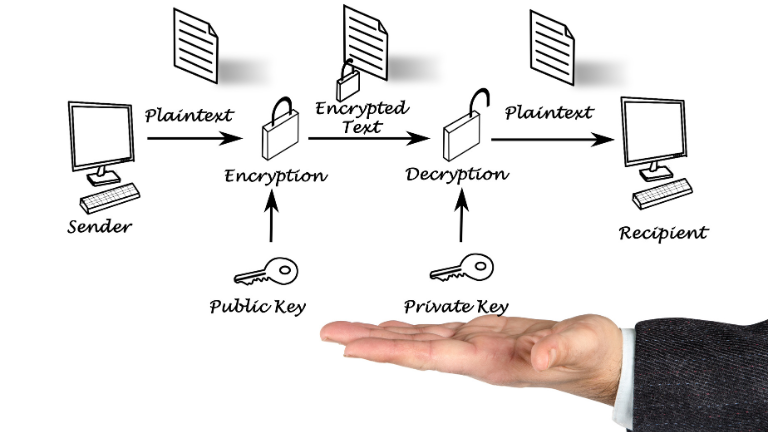
公開鍵暗号方式とは、公開鍵と秘密鍵を利用してデータのやり取りを行う暗号方式です。
データを解読するのに利用する鍵は公開鍵であり、秘密鍵はひとつしかない大切な鍵であると覚えておきましょう。
つまり公開鍵は誰に見られても問題なく、第三者にも公開されていることから公開鍵暗号方式と呼ばれています。
例として、公開鍵と秘密鍵を利用してデータを送信する手順を見てみましょう。
- 受信者は秘密鍵を使い、秘密鍵を作成する
- 送信者は受信者の公開鍵を取得する
- 送信者は暗号鍵を使い、暗号化したい文章を送信する
- 受信者は暗号文を受け取る
- 受信者は秘密鍵を使い、暗号文を平文にする
RSA暗号も、公開鍵暗号方式として利用されているアルゴリズムのひとつです。
鍵の交換や暗号化、後述するデジタル署名ができるアルゴリズムとして、世界で最初に登場しました。
RSA暗号の仕組み

ここまで、RSA暗号と公開鍵暗号方式をお伝えしました。
続いて、RSA暗号の仕組みを解説します。
- 受信者が公開鍵・秘密鍵を生成する
- 送信者がメッセージを暗号化する
- 受信者がメッセージを復号する
それぞれ詳しく解説していきます。
受信者が公開鍵・秘密鍵を生成する
RSA暗号の仕組みとして、まずは受信者が公開鍵・秘密鍵を生成します。
それぞれの鍵を生成する手順は、下記の通りです。
- 異なる2つの素数「p」「q」をとる
- n=pqとする
- (p-1)(q-1)と、それぞれ素の自然数であるk1をとる
- k1k2≡1(mod(p-1)(q-1))なるk2をとる
- nとk1を公開鍵として公開して、k2は秘密鍵として公開しない
上記手順の中にある「それぞれの素」とは、最大公約数1を意味します。
ちなみに、pとqも秘密鍵にあたるので公開しません。
送信者がメッセージを暗号化する
公開鍵・秘密鍵を生成できたら、送信者がメッセージを暗号化します。
メッセージを暗号化する手順は、下記の通りです。
- 送りたいメッセージをmとする(ただし、mはn未満の正の数とする)
- 公開鍵を使いmをk1乗してあとに、割った余りをC(暗号文)とする
算出されたC(暗号文)を、受信側に送信します。
受信者がメッセージを復号する
送信者のメッセージを暗号化できたら、受信者がメッセージを復号します。
メッセージを復号する手順は、「C(暗号文)k2(秘密鍵)を使い、Cをk2乗して、nで割る」です。
復号するにはk2(秘密鍵)が必要ですが、受信者しか持っていないので、第三者は復号できません。
またpとqも秘密鍵にあたるので、nからpとqを逆算するには素因数分解が必要です。
解読には膨大な時間と手間がかかるので、第三者の解読は現実的に不可能とされています。
▼人手不足でお悩みの方はこちらの記事がおすすめ!▼
RSA暗号の計算事例
ここまで、RSA暗号の仕組みをお伝えしました。
続いて、RSA暗号の計算事例を解説します。
- 公開鍵・秘密鍵の生成
- 暗号化の処理
- 復号の処理
ひとつずつ解説していきます。
公開鍵・秘密鍵の生成
まずは公開鍵・秘密鍵を生成するための準備をします。
計算事例ということで、下記に数字を割り当てていきましょう。
- p=23、q=31とする
- n=pq=713
- (23-1)(31-1)=22×30=660
- それぞれ素の自然数として、k1=7をとる
- 7×k2≡1mod660は、k2=283と一意する
公開鍵であるn=713とk1=7を公開して、k2=283を秘密鍵とします。
暗号化の処理
公開鍵・秘密鍵を生成できたら、暗号化の処理を行います。
送信者がメッセージ「478」を送ると仮定しましょう。
n=713として、478の7乗≡673です。
C=673として、送信します。
復号の処理
暗号化の処理が完了したら、復号の処理を行います。
n=713とすると、673の283乗≡483です。
以上で復号の処理ができました。
RSA暗号以外の暗号

ここまで、RSA暗号の計算事例をお伝えしました。
続いて、RSA暗号以外の暗号を解説します。
- DES(3DES)
- AES
- 楕円曲線暗号
- ハイブリッド暗号
ひとつずつ解説していきます。
DES(3DES)
DES(3DES)とはアメリカで規格化された、DES処理を3回繰り返す暗号アルゴリズムです。
ちなみにDESは、「Data Encryption Standard」の頭文字をとって名付けられました。
DES(3DES)の特徴は、下記の通りです。
- 8バイト(64ビット)の鍵を利用して、平文を複雑に処理して暗号化する
- 暗号の強度を高めるため、「暗号化→復号→暗号化」の順番で処理する
- 復号する際は、鍵を利用して逆の順番で一連の操作を行う
ただし現在は、ブルートフォース攻撃などで解読されるようになっており、後継であるAES(Advanced Encryption Standard)の利用が推奨されています。
また同じ処理を繰り返すことで、パソコンに大きな負荷になる点も要因のひとつです。
AES
AESとは、無線LANといった通信データを暗号化する際に利用されている暗号アルゴリズムです。
DES(3DES)の後継とされており、2001年に承認されて以来、今でも標準的に使用されています。
AESの特徴は、下記の通りです。
- 128・192・256ビットの中から鍵長を選べる
- SSL/TLS化通信やファイルの暗号化などにWPA2が利用されている
- SubBytesとShiftRows、MixColumns、AddRoundKeyに変換できる
セキュリティ強度が高いだけでなく、許諾や対価の支払いも必要な技術に含まれていません。
また、仕様も公開されているので多くの製品や暗号規格に広く普及しています。
楕円曲線暗号
楕円曲線暗号とは、有限体上の楕円曲線を利用した暗号アルゴリズムの総称です。
多くの場面では、公開鍵暗号として活用されています。
ビットコインの暗号化方式として採用されており、楕円曲線上にある離散対数問題における数学上の問題を安全性と根拠としています。
そんな楕円曲線暗号の特徴は、下記の通りです。
- 計算能力が高くないパソコンでも実装できる
- RSA暗号より短い鍵長で高い安全性を確保できる
一方で、アプリケーションやサービスの中にある、TLS/SSL証明書との相互運用はできません。
ハイブリッド暗号
ハイブリッド暗号とは、公開鍵と秘密鍵を組み合わせた暗号アルゴリズムです。
これまで、それぞれの鍵には「暗号化や復号の処理に時間がかかる」「鍵の管理が難しい」といった問題がありました。
そんなお互いの弱点を補っている暗号アルゴリズムが、ハイブリッド暗号です。
つまり第三者に復号鍵を盗まれる心配が少なく、鍵の送信にも時間がかかりません。
また、メールを暗号するS/MIMEなどでも実装されています。
こちらの記事では、インターネットを利用する際に目にするHTTPとHTTPSの違いを、セキュリティ・速度・役割の観点から解説しているので、ぜひ参考にしてください。
▼人手不足でお悩みの方はこちらの記事がおすすめ!▼
RSA暗号の応用事例

ここまで、RSA暗号以外の暗号をお伝えしました。
続いて、RSA暗号の応用事例を紹介します。
- 通信の暗号化
- デジタル署名
それぞれ紹介していきます。
通信の暗号化
RSA暗号は、通信の暗号化に活用されています。
具体的に活用されている通信プロトコルは、SSL(Secure Socket Layer)です。
SSLの特徴として、下記があげられます。
- Webサーバーとブラウザ間の通信プロトコルを暗号化する
- ファイルを転送する際のFTP技術にも採用されている
SSLを利用するブラウザには、電子証明書が組み込まれています。
また、サーバーからの情報は秘密鍵で暗号化されているので、ブラウザの公開鍵で復号したあとで参照が可能です。
こちらの記事では、通信方法である「FTP」特徴や転送方法、機能について解説しているので、ぜひ参考にしてください。
デジタル署名
RSA暗号は、デジタル署名にも応用されています。
デジタル署名とは、書類上の手書き署名と同じセキュリティ性が担保されている公開鍵暗号のひとつです。
デジタル署名の特徴には、下記の2つがあります。
- 第三者のなりすましによる署名・偽造を防げる
- 署名後の書面内容が改ざん・変造されるリスクがない
つまり、発信者の署名は秘密鍵で暗号化されているため、当人の署名である証明といえます。
まとめ

今回は、RSA暗号の概要や仕組み、応用事例を解説しました。
RSA暗号とは、現在のインターネットの基礎となっている素因数分解を利用した暗号アルゴリズムです。
具体的な仕組みは、下記の3つで成り立っています。
- 受信者が公開鍵・秘密鍵を生成する
- 送信者がメッセージを暗号化する
- 受信者がメッセージを復号する
また、公開鍵・秘密鍵の生成や暗号化、復号処理する際の計算事例もお伝えしました。
本記事でお伝えしたRSA暗号以外の暗号や応用事例も参考にして、セキュリティに対する知識を深めてください。
▼人手不足でお悩みの方はこちらの記事がおすすめ!▼
【SNSフォローのお願い】
kyozonは日常のビジネスをスマートにする情報を毎日お届けしています。
今回の記事が「役に立った!」という方はtwitterとfacebookもフォローいただければ幸いです。
twitter:https://twitter.com/kyozon_comix